自适应滤波器具有在未知环境下良好的运作并跟踪输入统计量随时间变化的能力。尽管对于不同的应用有不同的实现结构，但是他们都有一个基本的特征：输入向量X(n)和期望响应d(n)被用来计算估计误差e(n)，即e(n)=d(n)-X(n)，并利用此误差信号构造一个自适应算法的性能函数（比如均方误差MSE），并随数据的不断输入自适应地更新此性能函数，目标是最小化此性能函数，在此过程中不断地更新调整滤波器的滤波参数，使得这个参数在前面的最小化性能函数所使用的准则下最优，从而达到滤波效果，实现自适应过程。自适应滤波器主要应用有：预测、辨识、反建模、干扰抵消。
实现自适应滤波器的算法有很多，比较经典的有：LMS，RLS。其中LMS算法是属于梯度类算法，在1996年被Hassibi等证明了在准则下为最优，失调系数和收敛性可以通过合理的选取收敛因子u，但是如果输入相关矩阵的特征值比较分散时，算法的收敛性变差，故而后来又出现一些改进算法，比如NLMS。RLS是递推算法，准则是最小二乘准则，属于精确分析，相对于LMS滤波，RLS对于非平稳信号的适应性要强很多。
自适应滤波器可以由不同的结构来实现。目前主要有两种结构：FIR、IIR。前者也可以称为横向结构，易于实现，但是存在收敛性差的问题，后者主要是存在系统可能不稳定的问题。
根据一些matlab书籍上的例程做了一个LMS算法：
clear;
clc;
N=150;
length=10000;
t=0:1/(N+length):1-1/(N+length);
s=sin(4*pi*t);
n=randn(size(t));
x=s+n;
w=zeros(1,N);
e=zeros(1,length);
E=zeros(1,length);
u=0.00174;
for i=1:length
y(i)=x(i:i+N-1)*w';
e(i)=s(i)-y(i);
w=w+2*u*e(i)*x(i:i+N-1);
E(i)=e(i)*e(i);
end
figure(1);
subplot(3,1,1);
plot(t,x);
axis([0 1 -5 5]);
title('带噪声信号');
subplot(3,1,2);
plot(t,s);
axis([0 1 -1.1 1.1]);
title('期望信号');
subplot(3,1,3);
plot(0:1/(N+length):(length-1)/(N+length),y);
axis([0 1 -1.1 1.1]);
title('滤波后信号');
figure(2);
plot((1:length),E);
axis([0 10000 0 0.1]);
title('误差')
结果如下：
常用的自适应滤波技术有：最小均方（LMS）自适应滤波器、递推最小二乘（RLS）滤波器、格型滤波器和无限冲激响应（IIR）滤波器等。这些自适应滤波技术的应用又包括：自适应噪声抵消、自适应谱线增强和陷波等。首先介绍最小均方（LMS）自适应滤波器原理。
和干扰噪声
之和
阶滤波器的系数定义为![\mathbf{w}_{n}=\left[w_{n}(0),\,w_{n}(1),\, ...,\,w_{n}(p)\right]^{T}](http://upload.wikimedia.org/wikipedia/zh/math/0/7/4/074e16bf18eaa748719f59cd5b3152a0.png)
.
可变滤波器通过将输入信号与脉冲响应作卷积估计所要信号，用向量表示为
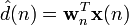
其中
![\mathbf{x}(n)=\left[x(n),\,x(n-1),\,...,\,x(n-p)\right]^{T}](http://upload.wikimedia.org/wikipedia/zh/math/f/e/d/fedd020ae481f4f2c183240369808107.png)
是输入信号向量。另外，可变滤波器每次都会马上改变滤波器系数
其中
是滤波器系数的校正因子。自适应算法根据输入信号与误差信号生成这个校正因子，LMS 和 RLS 是两种不同的系数更新算法。
LMS算法原理：
LMS自适应滤波器是使滤波器的输出信号与期望响应之间的误差的均方值为最小，因此称为最小均方（LMS）自适应滤波器。
【参考文献】
[1] 丁玉美，阔永红，高新波 A ． 数字信号处理-时域离散随机信号处理 [M] ．西安：西安电子科技大学出版社， 2002．
[2] 万建伟，王玲． 信号处理仿真技术 [M] ．长沙：国防科技大学出版社， 2008 ．
[3] 薛年喜． MATLAB在数字信号处理中的应用（第2版） [M] ．北京：清华大学出版社， 2008 ．
http://www.cnblogs.com/iqstudy/articles/1805482.html
评论